Optimization by Grid search

In this section, we will explain how to perform a grid-type search to analyze atomic coordinates from diffraction data. The grid type search is compatible with MPI. The specific calculation procedure is the same as for minsearch. It is necessary to prepare the data file MeshData.txt that defines the search grid in advance.

Location of the sample files

The sample files are located in sample/single_beam/mapper. The following files are stored in the folder:

• bulk.txt

  Input file of bulk.exe

• experiment.txt, template.txt

  Reference file to proceed with calculations in the main program.

• MeshData.txt

  Data file for the search grid.

• input.toml

  Input file of the main program.

• ref_ColorMap.txt

  A file to check if the calculation was performed correctly (the answer to ColorMap.txt obtained by doing this tutorial).

• prepare.sh, do.sh

  Script prepared for bulk calculation of this tutorial.

Below, we will describe these files and then show the actual calculation results.

Reference files

The template.txt and experiment.txt are the same as in the previous tutorial (Nealder-Mead optimization). Except, to reduce the computation time, the value of value_03 is fixed to 3.5 instead of the variable, and thus the grid is searched in two-dimensional space. The actual grid to be searched is given in MeshData.txt. In the sample, the contents of MeshData.txt are as follows.

1 6.000000 6.000000
2 6.000000 5.750000
3 6.000000 5.500000
4 6.000000 5.250000
5 6.000000 5.000000
6 6.000000 4.750000
7 6.000000 4.500000
8 6.000000 4.250000
9 6.000000 4.000000
...

The first column is the serial number, and the second and subsequent columns are the values of value_0, value_1, and so on that are referred to by the variables in template.txt in that order.

Input file

This section describes the input file for the main program, input.toml. The details of input.toml can be found in the input file section of the manual. The following is the content of input.toml in the sample file.

[base]
dimension = 2
output_dir = "output"

[solver]
name = "sim-trhepd-rheed"
run_scheme = "subprocess"
generate_rocking_curve = false

[solver.config]
cal_number = [1]

[solver.param]
string_list = ["value_01", "value_02" ]

[solver.post]
normalization = "TOTAL"

[solver.reference]
path = "experiment.txt"
exp_number = [1]

[algorithm]
name = "mapper"
label_list = ["z1", "z2"]

[algorithm.param]
mesh_path = "./MeshData.txt"

First, [base] section is explained.

• dimension is the number of variables to be optimized. In this case, it is 2 since we are optimizing two variables as described in template.txt.

• output_dir is the name of directory for the outputs. If it is omitted, the results are written in the directory in which the program is executed.

[solver] section specifies the solver to be used inside the main program and its settings.

• name is the name of the solver you want to use. In this tutorial it is sim-trhepd-rheed.

• run_scheme specifies how the solver is executed within the program. In the current version, subprocess can be specified.

The solver can be configured in the subsections [solver.config], [solver.param], and [solver.reference].

[solver.config] section specifies options for reading the output file produced by surf.exe that is called from the main program.

• calculated_first_line specifies the first line to read from the output file.

• calculated_last_line specifies the last line of the output file to be read.

• cal_number specifies the indices of columns of the output file to read.

[solver.param] section specifies options for the input file passed to surf.exe that is to be called from the main program.

• string_list is a list of variable names embedded in template.txt.

[solver.reference] section specifies the location of the experimental data and the range to read.

• path specifies the path where the experimental data is located.

• first specifies the first line of the experimental data file to read.

• end specifies the last line of the experimental data file to read.

• exp_number specifies the indices of columns of the experimental data file to read.

[algorithm] section specifies the algorithm to use and its settings.

• name is the name of the algorithm you want to use. In this tutorial we will use mapper since we will be using grid-search method.

• label_list is a list of label names to be attached to the output of value_0x (x=1,2).

For details on other parameters that can be specified in the input file, please see the Input File section of the manual.

Calculation execution

First, move to the folder where the sample files are located. (We assume that you are directly under the directory where you downloaded this software.)

$ cd sample/single_beam/mapper

Copy bulk.exe and surf.exe.

$ cp ../../sim-trhepd-rheed/src/bulk.exe .
$ cp ../../sim-trhepd-rheed/src/surf.exe .

Run bulk.exe to produce bulkP.b.

$ ./bulk.exe

After that, run the main program. The computation time will take only a few seconds on a normal PC.

$ mpiexec -np 2 odatse-STR input.toml | tee log.txt

Here, the calculation using MPI parallel with 2 processes will be done.

When executed, a folder for each rank will be created, and a subfolder LogXXXX_YYYY (where XXXX and YYYY are the grid id and the sequence number, respectively) will be created under it. (The grid id is associated to the index in MeshData.txt.) The standard output will look like as follows.

name            : mapper
label_list      : ['z1', 'z2']
param.mesh_path : ./MeshData.txt
Iteration : 1/66
Iteration : 2/66
Iteration : 3/66
Iteration : 4/66
Iteration : 5/66
Iteration : 6/66
...
Iteration : 63/66
Iteration : 64/66
Iteration : 65/66
Iteration : 66/66
[0] minimum_value: 1.51992524e-02 at [5.25, 4.25] (mesh 34)
Make ColorMap
complete main process : rank 00000000/00000001
end of run

Finally, the R-factor calculated at all the points on the grid will be written to ColorMap.txt. In this case, the following results will be obtained.

6.000000 6.000000 0.047852
6.000000 5.750000 0.055011
6.000000 5.500000 0.053190
6.000000 5.250000 0.038905
6.000000 5.000000 0.047674
6.000000 4.750000 0.065919
6.000000 4.500000 0.053675
6.000000 4.250000 0.061261
6.000000 4.000000 0.069351
6.000000 3.750000 0.071868
6.000000 3.500000 0.072739
...

The first and second columns contain the values of value_01 and value_02, and the third column contains the R-factor.

Note that do.sh is available as a script for batch calculation. In do.sh, res.txt and ref.txt are also compared for the check. Here is what it does, without further explanation.

#!/bin/sh

sh prepare.sh

./bulk.exe

time mpiexec -np 2 odatse-STR input.toml

echo diff output/ColorMap.txt ref_ColorMap.txt
res=0
diff output/ColorMap.txt ref_ColorMap.txt || res=$?
if [ $res -eq 0 ]; then
  echo TEST PASS
  true
else
  echo TEST FAILED: ColorMap.txt and ref_ColorMap.txt differ
  false
fi

Visualization of calculation results

By examining ColorMap.txt, we can estimate the region where the value of R-factor becomes small. In this case, the following command will create a two-dimensional parameter space diagram ColorMapFig.png.

$ python3 plot_colormap_2d.py

Looking at the generated figure, we can see that it has the minimum value around (5.25, 4.25).

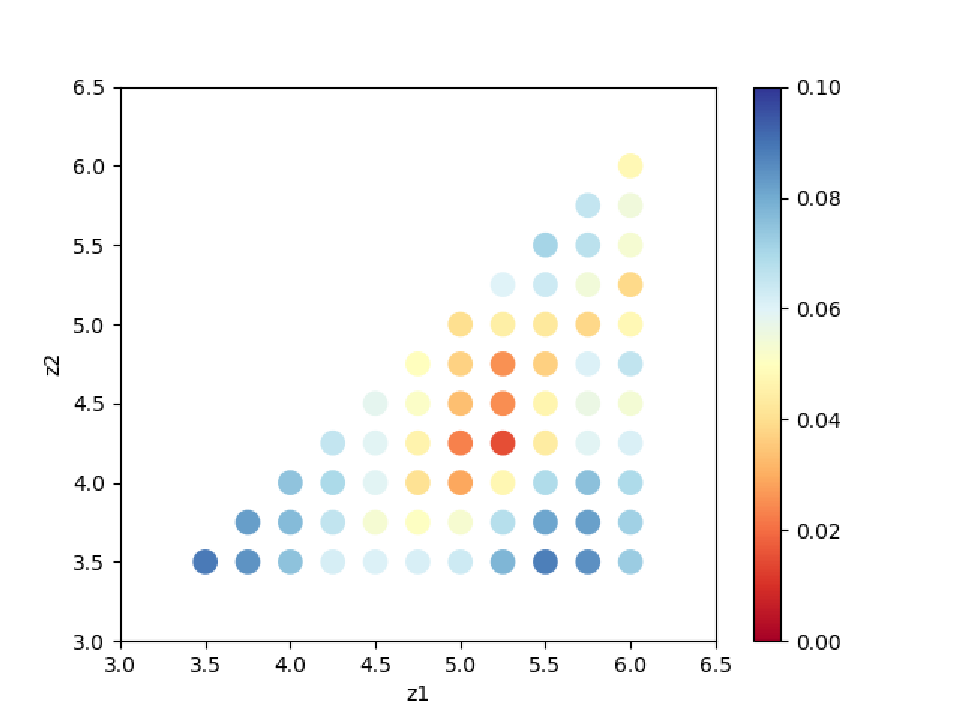
Fig. 4 R-factor on a two-dimensional parameter space.

When generate_rocking_curve in [solver] section is set to true, RockingCurve_calculated.txt will be generated in each log directory. By using it, you can compare the results with the experimental values following the procedure in the previous tutorial.