Optimization by Nelder-Mead method¶
In this section, we will explain how to calculate the inverse problem of analyzing atomic coordinates from diffraction data using the Nelder-Mead method. The specific calculation procedure is as follows.
Preparation of the reference file
Prepare the reference file to be matched (in this tutorial, it corresponds to
experiment.txtdescribed below).Perform calculations on the bulk part of the surface structure.
Copy
bulk.exetosample/minsearchand run the calculation.Run the main program
Run the calculation using
odatse-STRto estimate the atomic coordinates.
In the main program, the Nelder-Mead method implemented in scipy.optimize.fmin is applied to find the parameter that minimizes the deviation (R-value) between the intensity obtained using the solver (in this case surf.exe) and the intensity listed in the reference file (experiment.txt).
Location of the sample files¶
The sample files are located in sample/single_beam/minsearch.
The following files are stored in the folder.
bulk.txtInput file of
bulk.exe.experiment.txt,template.txtReference file to proceed with calculations in the main program.
ref.txtA file containing the answers you want to seek in this tutorial.
input.tomlInput file of the main program.
prepare.sh,do.shScript prepared for doing all calculation of this tutorial
The following sections describe these files and then show the actual calculation results.
The reference file¶
The template.txt file is almost the same format as the input file for surf.exe.
The parameters to vary (such as the atomic coordinates you want to find) are labeled as value_* or some other appropriate strings.
The following is the content of template.txt.
2 ,NELMS, -------- Ge(001)-c4x2
32,1.0,0.1 ,Ge Z,da1,sap
0.6,0.6,0.6 ,BH(I),BK(I),BZ(I)
32,1.0,0.1 ,Ge Z,da1,sap
0.4,0.4,0.4 ,BH(I),BK(I),BZ(I)
9,4,0,0,2, 2.0,-0.5,0.5 ,NSGS,msa,msb,nsa,nsb,dthick,DXS,DYS
8 ,NATM
1, 1.0, 1.34502591 1 value_01 ,IELM(I),ocr(I),X(I),Y(I),Z(I)
1, 1.0, 0.752457792 1 value_02
2, 1.0, 1.480003343 1.465005851 value_03
2, 1.0, 2 1.497500418 2.281675
2, 1.0, 1 1.5 1.991675
2, 1.0, 0 1 0.847225
2, 1.0, 2 1 0.807225
2, 1.0, 1.009998328 1 0.597225
1,1 ,(WDOM,I=1,NDOM)
In this input file, value_01, value_02, and value_03 are used.
In the sample folder, there is a reference file ref.txt to know if the atomic positions are estimated correctly. The contents of this file are
fx = 8.97501627575891e-06
z1 = 5.230573154947887
z2 = 4.3706085364407095
z3 = 3.5961303342247577
value_01, value_02, and value_03 correspond to z1, z2, and z3, respectively.
fx is the optimal value of the objective function.
experiment.txt is a file that is used as a reference in the main program.
In this tutorial, it is equivalent to convolution.txt obtained from the calculation when putting the parameters in ref.txt into template.txt and following the same procedure as in the tutorial on direct problems.
(Note that they are different from those in the tutorial of the direct problem because the input files for bulk.exe and surf.exe are different.)
Input files¶
In this section, we prepare the input file input.toml for the main program.
The details can be found in the input file section in the manual.
The content of input.toml is shown below.
[base]
dimension = 3
output_dir = "output"
[solver]
name = "sim-trhepd-rheed"
run_scheme = "subprocess"
generate_rocking_curve = true
[solver.config]
cal_number = [1]
[solver.param]
string_list = ["value_01", "value_02", "value_03" ]
[solver.reference]
path = "experiment.txt"
exp_number = [1]
[solver.post]
normalization = "TOTAL"
[algorithm]
name = "minsearch"
label_list = ["z1", "z2", "z3"]
[algorithm.param]
min_list = [0.0, 0.0, 0.0]
max_list = [10.0, 10.0, 10.0]
initial_list = [5.25, 4.25, 3.50]
First, [base] section is explained.
dimensionis the number of variables to be optimized. In this case it is3since we are optimizing three variables as described intemplate.txt.output_diris the name of directory for the outputs. If it is omitted, the results are written in the directory in which the program is executed.
[solver] section specifies the solver to be used inside the main program and its settings.
nameis the name of the solver you want to use. In this tutorial it issim-trhepd-rheed.run_schemespecifies how the solver is executed within the program. In the current version,subprocesscan be specified.generate_rocking_curvespecifies whether or not the rocking curves are generated in every steps.
The solver can be configured in the subsections [solver.config], [solver.param], and [solver.reference].
[solver.config] section specifies options for reading the output file produced by surf.exe that is called from the main program.
calculated_first_linespecifies the first line to read from the output file.calculated_last_linespecifies the last line of the output file to be read.cal_numberspecifies the indices of columns of the output file to read.
[solver.param] section specifies options for the input file passed to surf.exe that is to be called from the main program.
string_listis a list of variable names embedded intemplate.txt.
[solver.reference] section specifies the location of the experimental data and the range to read.
pathspecifies the path where the experimental data is located.firstspecifies the first line of the experimental data file to read.endspecifies the last line of the experimental data file to read.exp_numberspecifies the indices of columns of the experimental data file to read.
[algorithm] section specifies the algorithm to use and its settings.
nameis the name of the algorithm you want to use. In this tutorial, it is set tominsearch, since we are using the Nelder-Mead method.label_listis a list of label names to be attached to the output ofvalue_0x(x=1,2,3).
[algorithm.param] section specifies the range of parameters to search and their initial values.
min_listandmax_listspecify the minimum and maximum values of the search range, respectively.initial_listspecifies the initial values.
Other parameters, such as convergence criteria used in the Nelder-Mead method, can be set in the [algorithm] section, although they are omitted here so that the default values are used.
See the input file section of the manual for details.
Calculation execution¶
First, move to the folder where the sample files are located. (We assume that you are directly under the directory where you downloaded this software.)
$ cd sample/single_beam/minsearch
Copy bulk.exe and surf.exe.
$ cp ../../sim-trhepd-rheed/src/bulk.exe .
$ cp ../../sim-trhepd-rheed/src/surf.exe .
Run bulk.exe to produce bulkP.b.
$ ./bulk.exe
After that, run the main program. The computation time will take only a few seconds on a normal PC.
$ odatse-STR input.toml | tee log.txt
Then, the standard output will look as follows.
name : minsearch
label_list : ['z1', 'z2', 'z3']
param.min_list : [0.0, 0.0, 0.0]
param.max_list : [10.0, 10.0, 10.0]
param.initial_list: [5.25, 4.25, 3.5]
eval: x=[5.25 4.25 3.5 ], fun=0.015199252435883206
eval: x=[5.22916667 4.3125 3.64583333], fun=0.013702918645281299
eval: x=[5.22569444 4.40625 3.54513889], fun=0.01263527811899235
eval: x=[5.17997685 4.34895833 3.5943287 ], fun=0.006001659635528168
eval: x=[5.17997685 4.34895833 3.5943287 ], fun=0.006001659635528168
eval: x=[5.22066294 4.33260995 3.60408629], fun=0.005145496928704404
eval: x=[5.22066294 4.33260995 3.60408629], fun=0.005145496928704404
eval: x=[5.2185245 4.32627234 3.56743818], fun=0.0032531465329236025
...
x= are the candidate parameters at each step, and fun= is the R-factor value at that point.
The results at each step are also written in the folder output/LogXXXX_YYYY (where XXXX and YYYY are the step counts).
The final estimated parameters will be written to output/res.dat.
In the current case, the following result will be obtained:
z1 = 5.230573154947887
z2 = 4.3706085364407095
z3 = 3.5961303342247577
You can see that we will get the same values as the correct answer data in ref.txt.
Note that do.sh is available as a script for batch calculation.
In do.sh, res.txt and ref.txt are also compared for the check.
Here is what it does, without further explanation.
#!/bin/sh
sh ./prepare.sh
./bulk.exe
time odatse-STR input.toml | tee log.txt
echo diff output/res.txt ref.txt
res=0
diff output/res.txt ref.txt || res=$?
if [ $res -eq 0 ]; then
echo Test PASS
true
else
echo Test FAILED: res.txt and ref.txt differ
false
fi
Visualization of calculation results¶
If generate_rocking_curve is set to true, the data of the rocking curve at each step is stored in LogXXXX_00000001 (where XXXX is the index of steps) as RockingCurve.txt.
A tool draw_RC_double.py is provided to visualize this data.
In this section, we will use this tool to visualize the results.
$ cp output/0/Log00000000_00000000/RockingCurve.txt RockingCurve_ini.txt
$ cp output/0/Log00000117_00000000/RockingCurve.txt RockingCurve_con.txt
$ cp ../../../script/draw_RC_double.py .
$ python3 draw_RC_double.py
By running the above, RC_double.png will be generated.
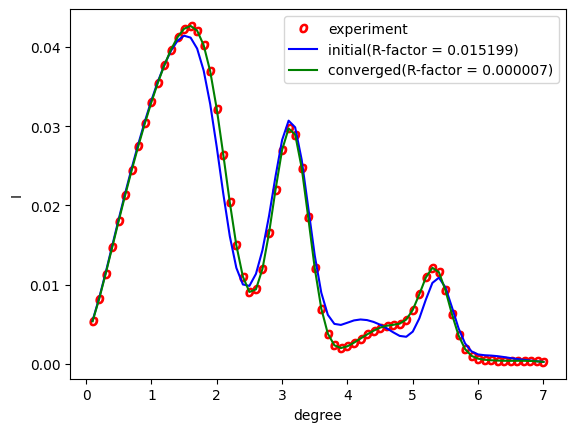
Fig. 3 Analysis using the Nelder-Mead method. The red circles represent the experimental values, the blue line represents the rocking curve at the first step, and the green line represents the rocking curve obtained at the last step.¶
From the figure, we can see that at the last step the result agrees with the experimental data.