Nelder-Mead法による最適化¶
ここでは、Nelder-Mead法を用いて回折データから原子座標を解析する逆問題の計算を行う方法について説明します。 具体的な計算手順は以下の通りです。
参照ファイルの準備
合わせたい参照ファイル (今回は後述する
experiment.txtに相当)を準備する。表面構造のバルク部分に関する計算実行
bulk.exeをsample/minsearchにコピーして計算を実行する。メインプログラムの実行
odatse-STRを用いて計算を実行し原子座標を推定する。
メインプログラムでは、Nelder-Mead法 (scipy.optimize.minimize を使用)を用いて、ソルバー(今回は surf.exe )を用いて得られた強度と、参照ファイル(experiment.txt)に記載された強度のずれ(R値)を最小化するパラメータを探索します。
サンプルファイルの場所¶
サンプルファイルは sample/single_beam/minsearch にあります。
フォルダには以下のファイルが格納されています。
bulk.txtbulk.exeの入力ファイルexperiment.txt,template.txtメインプログラムでの計算を進めるための参照ファイル
ref.txt本チュートリアルで求めたい回答が記載されたファイル
input.tomlメインプログラムの入力ファイル
prepare.sh,do.sh本チュートリアルを一括計算するために準備されたスクリプト
以下、これらのファイルについて説明したあと、実際の計算結果を紹介します。
参照ファイルの説明¶
template.txt は surf.exe の入力ファイルとほぼ同じ形式のファイルです。
動かすパラメータ(求めたい原子座標などの値)を「 value_* 」などの適当な文字列に書き換えています。
以下が template.txt の中身です。
2 ,NELMS, -------- Ge(001)-c4x2
32,1.0,0.1 ,Ge Z,da1,sap
0.6,0.6,0.6 ,BH(I),BK(I),BZ(I)
32,1.0,0.1 ,Ge Z,da1,sap
0.4,0.4,0.4 ,BH(I),BK(I),BZ(I)
9,4,0,0,2, 2.0,-0.5,0.5 ,NSGS,msa,msb,nsa,nsb,dthick,DXS,DYS
8 ,NATM
1, 1.0, 1.34502591 1 value_01 ,IELM(I),ocr(I),X(I),Y(I),Z(I)
1, 1.0, 0.752457792 1 value_02
2, 1.0, 1.480003343 1.465005851 value_03
2, 1.0, 2 1.497500418 2.281675
2, 1.0, 1 1.5 1.991675
2, 1.0, 0 1 0.847225
2, 1.0, 2 1 0.807225
2, 1.0, 1.009998328 1 0.597225
1,1 ,(WDOM,I=1,NDOM)
今回の入力ファイルでは、 value_01, value_02, value_03 を用いています。
サンプルフォルダには、原子位置が正しく推定できているかを知るための参照ファイルとして、
ref.txt が置いてあります。ファイルの中身は
fx = 8.97501627575891e-06
z1 = 5.230573154947887
z2 = 4.3706085364407095
z3 = 3.5961303342247577
となっており、 value_01, value_02, value_03 がそれぞれ z1, z2, z3 に対応しています。
fx は目的関数の最適値です。
experiment.txt は、メインプログラムで参照に用いるファイルです。ここではテストデータとして、
template.txt に ref.txt のデータを代入し、順問題のチュートリアルと同様な手順で計算して得られる convolution.txt に相当しています。
(順問題のチュートリアルとは bulk.exe , surf.exe の入力ファイルが異なるのでご注意ください。)
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml の準備をします。
input.toml の詳細については入力ファイルに記載されています。
ここでは、サンプルファイルにある input.toml の中身について説明します。
[base]
dimension = 3
output_dir = "output"
[solver]
name = "sim-trhepd-rheed"
run_scheme = "subprocess"
generate_rocking_curve = true
[solver.config]
cal_number = [1]
[solver.param]
string_list = ["value_01", "value_02", "value_03" ]
[solver.reference]
path = "experiment.txt"
exp_number = [1]
[solver.post]
normalization = "TOTAL"
[algorithm]
name = "minsearch"
label_list = ["z1", "z2", "z3"]
[algorithm.param]
min_list = [0.0, 0.0, 0.0]
max_list = [10.0, 10.0, 10.0]
initial_list = [5.25, 4.25, 3.50]
最初に [base] セクションについて説明します。
dimensionは最適化したい変数の個数で、今の場合はtemplate.txtで説明したように3つの変数の最適化を行うので、3を指定します。output_dirは出力先のディレクトリ名です。省略した場合はプログラムを実行したディレクトリになります。
[solver] セクションではメインプログラムの内部で使用するソルバーとその設定を指定します。
nameは使用したいソルバーの名前です。sim-trhepd-rheedに固定されています。run_schemeはソルバーを実行する方法の指定です。subprocessのみ指定可能です。generate_rocking_curveは実行ステップごとに Rocking Curve を出力するかどうかを指定します。
ソルバーの設定は、サブセクションの [solver.config], [solver.param], [solver.reference], [solver.post] で行います。
[solver.config] セクションではメインプログラム内部で呼び出す surf.exe により得られた出力ファイルを読み込む際のオプションを指定します。
cal_numberは出力ファイルの何列目を読み込むかを指定します。
[solver.param] セクションではメインプログラム内部で呼び出す surf.exe への入力パラメータについてのオプションを指定します。
string_listは、template.txtに記述する、動かしたい変数の名前のリストです。
[solver.reference] セクションでは、実験データの置いてある場所と読みこむ範囲を指定します。
pathは実験データが置いてあるパスを指定します。exp_numberは実験データファイルの何列目を読み込むかを指定します。
[solver.post] セクションでは、後処理のオプションを指定します。
normalizationは複数ビームの規格化を指定します。
[algorithm] セクションでは、使用するアルゴリスムとその設定をします。
nameは使用したいアルゴリズムの名前で、このチュートリアルでは、Nelder-Mead法 を用いた解析を行うので、minsearchを指定します。label_listは、value_0x(x=1,2,3) を出力する際につけるラベル名のリストです。
[algorithm.param] セクションでは、探索するパラメータの範囲や初期値を指定します。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。initial_listは初期値を指定します。
ここではデフォルト値を用いるため省略しましたが、その他のパラメータ、例えばNelder-Mead法で使用する収束判定などについては、 [algorithm] セクションで行うことが可能です。
詳細については入出力の章をご覧ください。
計算実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します).
$ cd sample/single_beam/minsearch
順問題の時と同様に、 bulk.exe と surf.exe をコピーします。
$ cp ../../sim-trhepd-rheed/src/bulk.exe .
$ cp ../../sim-trhepd-rheed/src/surf.exe .
bulk.exe を実行し、 bulkP.b を作成します。
$ ./bulk.exe
そのあとに、メインプログラムを実行します(計算時間は通常のPCで数秒程度で終わります)。
$ odatse-STR input.toml | tee log.txt
実行すると、以下の様な出力がされます。
name : minsearch
label_list : ['z1', 'z2', 'z3']
param.min_list : [0.0, 0.0, 0.0]
param.max_list : [10.0, 10.0, 10.0]
param.initial_list: [5.25, 4.25, 3.5]
eval: x=[5.25 4.25 3.5 ], fun=0.015199252435883206
eval: x=[5.22916667 4.3125 3.64583333], fun=0.013702918645281299
eval: x=[5.22569444 4.40625 3.54513889], fun=0.01263527811899235
eval: x=[5.17997685 4.34895833 3.5943287 ], fun=0.006001659635528168
eval: x=[5.17997685 4.34895833 3.5943287 ], fun=0.006001659635528168
eval: x=[5.22066294 4.33260995 3.60408629], fun=0.005145496928704404
eval: x=[5.22066294 4.33260995 3.60408629], fun=0.005145496928704404
eval: x=[5.2185245 4.32627234 3.56743818], fun=0.0032531465329236025
...
x= に各ステップでの候補パラメータと、その時のR-factorの値 fun= が出力されます。
また各ステップでの計算結果は output/0/LogXXXX_YYYY (XXXX, YYYYはステップ数)のフォルダに出力されます。
最終的に推定されたパラメータは、 output/res.dat に出力されます。今の場合、
z1 = 5.230573154947887
z2 = 4.3706085364407095
z3 = 3.5961303342247577
が得られ、正解のデータ ref.txt と同じ値が得られていることがわかります。
なお、一括計算するスクリプトとして do.sh を用意しています。
do.sh では output/res.txt と ref.txt の差分も比較しています。
以下、説明は割愛しますが、その中身を掲載します。
#!/bin/sh
sh ./prepare.sh
./bulk.exe
time odatse-STR input.toml | tee log.txt
echo diff output/res.txt ref.txt
res=0
diff output/res.txt ref.txt || res=$?
if [ $res -eq 0 ]; then
echo Test PASS
true
else
echo Test FAILED: res.txt and ref.txt differ
false
fi
計算結果の可視化¶
それぞれのステップでのロッキングカーブのデータは、 output/0/LogXXXX_00000001 (XXXX はステップ数)フォルダに RockingCurve.txt として保存されています
(output/0/LogXXXX_00000000 フォルダはNelder-Mead 法の途中での評価です)。
このデータを可視化するツール draw_RC_double.py が用意されています。
ここでは、このツールを利用して結果を可視化します。
$ cp output/0/Log00000000_00000000/RockingCurve_calculated.txt RockingCurve_ini.txt
$ cp output/0/Log00000117_00000000/RockingCurve_calculated.txt RockingCurve_con.txt
$ cp ../../../script/draw_RC_double.py .
$ python3 draw_RC_double.py
上記を実行すると RC_double.png が出力されます。
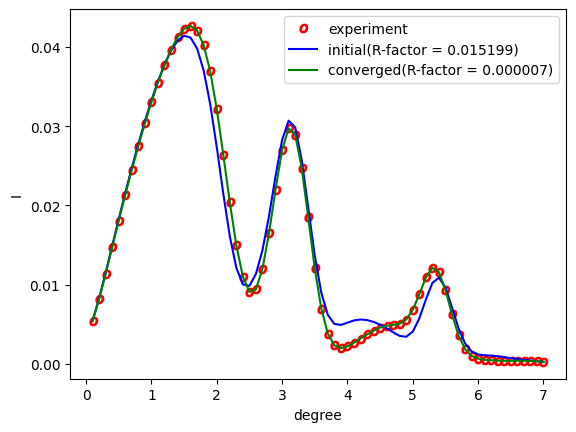
Nelder-Mead法を用いた解析。赤丸が実験値、青線が最初のステップ、緑線が最後のステップで得られたロッキングカーブを表す。¶
図から最後のステップでは実験値と一致していることがわかります。