グリッド型探索¶
ここでは、グリッド型探索を行い、回折データから原子座標を解析する方法について説明します。
グリッド型探索はMPIに対応しています。具体的な計算手順は minsearch の時と同様です。
ただし、探索グリッドを与えるデータ MeshData.txt を事前に準備する必要があります。
サンプルファイルの場所¶
サンプルファイルは sample/single_beam/mapper にあります。
フォルダには以下のファイルが格納されています。
bulk.txtbulk.exeの入力ファイルexperiment.txt,template.txtメインプログラムでの計算を進めるための参照ファイル
MeshData.txt探索グリッドのデータ
ref_ColorMap.txt計算が正しく実行されたか確認するためのファイル(本チュートリアルを行うことで得られる
ColorMap.txtの回答)。input.tomlメインプログラムの入力ファイル
prepare.sh,do.sh本チュートリアルを一括計算するために準備されたスクリプト
以下、これらのファイルについて説明したあと、実際の計算結果を紹介します。
参照ファイルの説明¶
template.txt , experiment.txt については、Nelder-Mead法による最適化と同じものを使用します。
ただし、計算を軽くするため value_03 は用いずに 3.5 に固定し、
2次元のグリッド探索を行うように変更してあります。
実際に探索するグリッドは MeshData.txt で与えます。
サンプルでは MeshData.txt の中身は以下のようになっています。
1 6.000000 6.000000
2 6.000000 5.750000
3 6.000000 5.500000
4 6.000000 5.250000
5 6.000000 5.000000
6 6.000000 4.750000
7 6.000000 4.500000
8 6.000000 4.250000
9 6.000000 4.000000
...
1列目が通し番号、2列目以降は template.txt に入る value_0, value_1 の値が順に指定されています。
入力ファイルの説明¶
ここでは、メインプログラム用の入力ファイル input.toml について説明します。
input.toml の詳細については入力ファイルに記載されています。
以下は、サンプルファイルにある input.toml の内容です。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "sim-trhepd-rheed"
run_scheme = "subprocess"
generate_rocking_curve = false
[solver.config]
cal_number = [1]
[solver.param]
string_list = ["value_01", "value_02" ]
[solver.post]
normalization = "TOTAL"
[solver.reference]
path = "experiment.txt"
exp_number = [1]
[algorithm]
name = "mapper"
label_list = ["z1", "z2"]
[algorithm.param]
mesh_path = "./MeshData.txt"
最初に [base] セクションについて説明します。
dimensionは最適化したい変数の個数で、今の場合はtemplate.txtで説明したように2つの変数の最適化を行うので、2を指定します。output_dirは出力先のディレクトリ名です。省略した場合はプログラムを実行したディレクトリになります。
[solver] セクションではメインプログラムの内部で使用するソルバーとその設定を指定します。
nameは使用したいソルバーの名前です。sim-trhepd-rheedに固定されています。run_schemeはソルバーを実行する方法の指定です。subprocessのみ指定可能です。
ソルバーの設定は、サブセクションの [solver.config], [solver.param], [solver.reference], [solver.post] で行います。
[solver.config] セクションではメインプログラム内部で呼び出す surf.exe により得られた出力ファイルを読み込む際のオプションを指定します。
cal_numberは出力ファイルの何列目を読み込むかを指定します。
[solver.param] セクションではメインプログラム内部で呼び出す surf.exe への入力パラメータについてのオプションを指定します。
string_listは、template.txtで読み込む、動かしたい変数の名前のリストです。
[solver.reference] セクションでは、実験データの置いてある場所と読みこむ範囲を指定します。
pathは実験データが置いてあるパスを指定します。exp_numberは実験データファイルの何列目を読み込むかを指定します。
[solver.post] セクションでは、後処理のオプションを指定します。
normalizationは複数ビームの規格化を指定します。
[algorithm] セクションでは、使用するアルゴリスムとその設定をします。
nameは使用したいアルゴリズムの名前で、このチュートリアルでは、グリッド探索による解析を行うので、mapperを指定します。label_listは、value_0x(x=1,2) を出力する際につけるラベル名のリストです。
[algorithm.param] セクションでは、探索するパラメータの範囲や初期値を指定します。
mesh_pathは、探索グリッドを記述するファイルを指定します。
その他、入力ファイルで指定可能なパラメータの詳細については入出力の章をご覧ください。
計算実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します).
$ cd sample/single_beam/mapper
順問題の時と同様に、 bulk.exe と surf.exe をコピーします。
$ cp ../../sim-trhepd-rheed/src/bulk.exe .
$ cp ../../sim-trhepd-rheed/src/surf.exe .
bulk.exe を実行し、 bulkP.b を作成します。
$ ./bulk.exe
そのあとに、メインプログラムを実行します(計算時間は通常のPCで数秒程度で終わります)。
$ mpiexec -np 2 odatse-STR input.toml | tee log.txt
ここではプロセス数2のMPI並列を用いた計算を行っています。
実行すると、output ディレクトリ内に各ランクのフォルダが作成され、その中にグリッドのidがついたサブフォルダ LogXXXX_00000000 (XXXX がグリッドのid) が作成されます
(MeshData.txt に付けられた番号がグリッドのidとして割り振られます)。
以下の様な出力が標準出力に書き出されます。
name : mapper
label_list : ['z1', 'z2']
param.mesh_path : ./MeshData.txt
Iteration : 1/66
Iteration : 2/66
Iteration : 3/66
Iteration : 4/66
Iteration : 5/66
Iteration : 6/66
...
Iteration : 63/66
Iteration : 64/66
Iteration : 65/66
Iteration : 66/66
[0] minimum_value: 1.51992524e-02 at [5.25, 4.25] (mesh 34)
Make ColorMap
complete main process : rank 00000000/00000001
end of run
最終的にグリッド上の全ての点で計算された R-factor は output/ColorMap.txt に出力されます。
今回の場合は
6.000000 6.000000 0.047852
6.000000 5.750000 0.055011
6.000000 5.500000 0.053190
6.000000 5.250000 0.038905
6.000000 5.000000 0.047674
6.000000 4.750000 0.065919
6.000000 4.500000 0.053675
6.000000 4.250000 0.061261
6.000000 4.000000 0.069351
6.000000 3.750000 0.071868
6.000000 3.500000 0.072739
...
のように得られます。1列目、2列目に value_01, value_02 の値が、3列目に R-factor が記載されます。
なお、一括計算するスクリプトとして do.sh を用意しています。
do.sh では ColorMap.dat と ref_ColorMap.dat の差分も比較しています。
以下、説明は割愛しますが、その中身を掲載します。
#!/bin/sh
sh prepare.sh
./bulk.exe
time mpiexec -np 2 odatse-STR input.toml
echo diff output/ColorMap.txt ref_ColorMap.txt
res=0
diff output/ColorMap.txt ref_ColorMap.txt || res=$?
if [ $res -eq 0 ]; then
echo TEST PASS
true
else
echo TEST FAILED: ColorMap.txt and ref_ColorMap.txt differ
false
fi
計算結果の可視化¶
ColorMap.txt を図示することで、 R-factor の小さいパラメータがどこにあるかを推定することができます。
以下のコマンドを入力すると、2次元パラメータ空間の図 ColorMapFig.png が作成されます。
$ python3 plot_colormap_2d.py
作成された図を見ると、(5.25, 4.25) 付近に最小値があることがわかります。
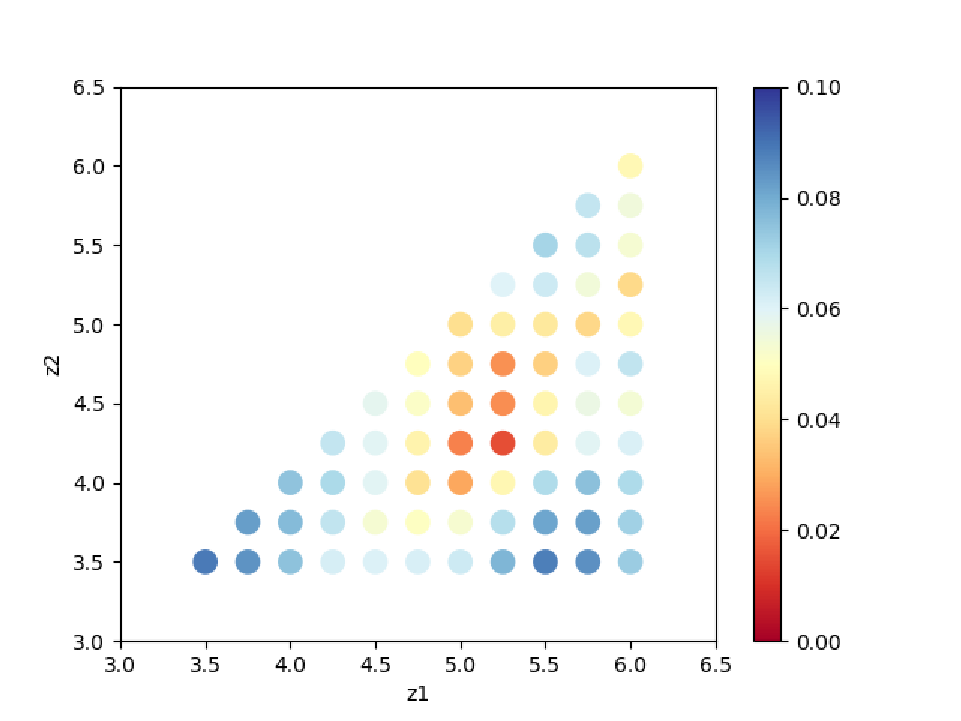
2次元パラメータ空間上での R-factor 。¶
また、 [solver] セクションの generate_rocking_curve パラメータを true にすると、各Logディレクトリに RockingCurve_calculated.txt が書き出されます。
これを用いることで、前チュートリアルの手順に従い、実験値との比較も行うことが可能です。